Калькулятор

Форсунка RUSA предназначена для работы в составе виброгрохота, решает задачу качественного распыления воды и увлажнения породы. Форсунка устанавливается неподвижно, увлажняемая порода движется мимо форсунки. Для увлажнения полосы породы необходимой ширины устанавливают несколько форсунок в ряд, при необходимости для более сильного увлажнения устанавливают несколько рядов форсунок. Общий вид форсунки и установка увлажняющих форсунок в составе виброгрохота иллюстрируют следующие рисунки:

Исходя из фотографий (Рис.2 и 3) работы форсунок, можно сделать следующее допущение о распределении воды по площади орошаемой породы:

• форсунка распределяет воду вдоль отрезка узкой линии
• форсунка распределяет воду равномерно

Обычно форсунку располагают так, чтобы линия орошения была перпендикулярна направлению движения породы. Если расход воды через форсунку известен, то с использованием этого предположения расчёт увлажнения породы сводится к решению геометрической задачи.

Объёмный расход воды можно определить, зная сечение форсунки S_СОПЛА (6 или 9 мм.) и  используя формулу Бернулли для нахождения скорости движения воды в выходном сечении форсунки:

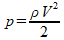
откуда

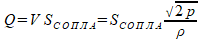
Здесь:

p – избыточное давление в подающем трубопроводе, Па. Величину давления в атмосферах необходимо домножить на 101300 (Па/ати), в барах - на 100000 (Па/бар);

V – скорость движения воды, м/сек. В расчёте буква V будет также использоваться для обозначения скорости движения породы относительно сопла.

ρ – плотность воды, кг/м³. Допустимо при всех температурах принимать ρ = 1000 кг/м³.

S_СОПЛА – сечение форсунки. Для использования в формуле необходимо взять величину в м². Для использования значений в мм2 их надо домножить на 10^-6 (мм²/м²).

Q – объёмный расход, м³/с. Для получения л/с необходимо домножить на 1000 (л/м³), для получения л/мин необходимо домножить на 60000 (л·сек/м³·мин).

Полученный расход воды равномерно распределяется на отрезок длины L, через который проезжает порода со скоростью V_ПОРОДЫ. Сначала рассмотрим простой случай, когда ось форсунки установлена вертикально, а линия орошения строго перпендикулярна направлению движения породы.

На рисунке схематично показана форсунка и создаваемый ею «факел» (скорее, плоский «веер») воды – вид сбоку и в направлении, перпендикулярном треугольному «лотку» форсунки, формирующему плоскую струю воды, треугольную в плане.

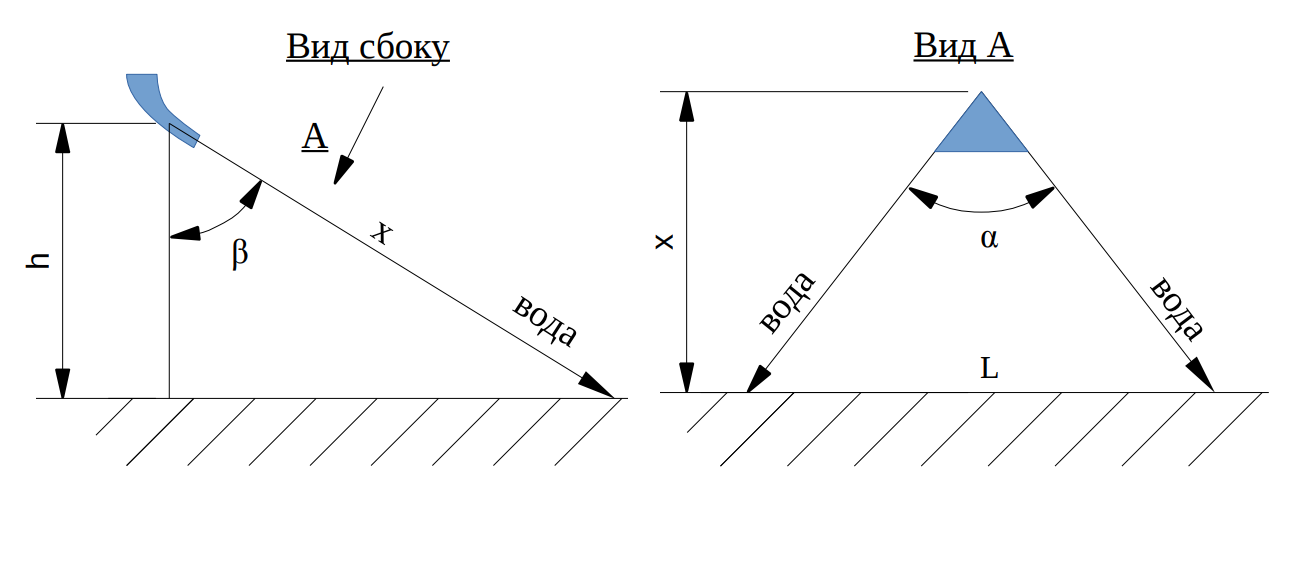
Обозначим:

h – высоту установки форсунки над орошаемой поверхностью,

L – ширина орошаемого форсункой отрезка,

x – «минимальная» длина пути воды от форсунки до поверхности, минимальный путь расположен перпендикулярно отрезку L,

α – угол раствора треугольного распыляющего лотка форсунки, измеренного в своей собственной плоскости,

β – угол отклонения плоскости, в которой распыляется вода, от вертикали.

Величины L и h являются переменными, остальные – конструктивные характеристики форсунки. Из двух рисунков видим, что

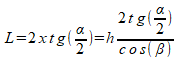
Формула даёт связь между высотой установки форсунки и длиной орошаемого отрезка. Коэффициент пропорциональности учитывает конструктивные особенности форсунки и вычисляется один раз.

Тогда «интенсивность орошения» – объём воды, получаемый единицей площади поверхности, вычисляется по формуле

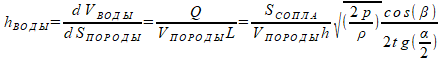
Здесь введено обозначение

h_ВОДЫ – количество «осадков» в метрах; для получения величины сантиметрах необходимо результат домножить на 100 (см/м), для получения величины миллиметрах необходимо результат домножить на 1000 (мм/м).

Формула связывает интенсивность орошения с сечением сопла, скоростью движения породы, высотой установки форсунок и рабочим давлением воды.

Возможен более сложный случай установки форсунок, когда входная трубка форсунки располагается с отклонением от вертикали. Возможно также отклонение отрезка распыления от направления, перпендикулярного скорости движения породы. Обозначим:

γ – угол дополнительного отклонения форсунки от вертикали. Он может быть как положительным, так и отрицательным. За положительное направление угла принимается такое, когда отклонение струи от вертикали вследствие наличия угла β у форсунки увеличивается, т. е. струя становится более горизонтальной. За отрицательное направление γ принимается противоположное направление, т. е. когда наклон форсунки начинает компенсировать наличие угла β и веер распыления становится более вертикальным.

Θ – угол между перпендикуляром к скорости движения и направлением отрезка распыления L.

Влияние обоих углов на вычисленные результаты учитывается следующим образом. Угол γ изменяет конструктивную величину угла β, а полоса распыления L сужается на множитель cos(Θ). Т.е. расчётные формулы модифицируются следующим образом:

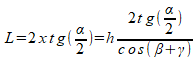
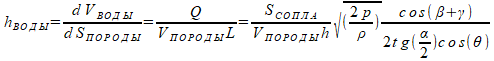
Используя полученные формулы, можем решить задачи о выборе необходимых параметров системы орошения для виброгрохота.

Во всех алгоритмах введена дополнительная величина:

δ – процент перекрытия соседних полос орошения. Может быть представлена в процентах, в формулах следует использовать значение из диапазона [0,1].

На эту величину сокращается расчётная полоса орошения:

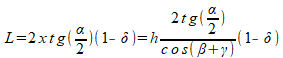
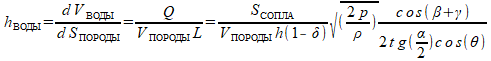
Вводим обозначения исходных данных:

L_{ГРОХОТА} – ширина орошаемой полосы виброгрохота, м;

H_ВОДЫ – требуемая по технологическому процессу интенсивность увлажнения, м. Если требуемое увлажнение было задано в миллиметрах, его величину следует поделить на 1000 (мм/м), если требуемое увлажнение было задано в сантиметрах, его величину следует поделить на 100 (см/м).

Приведём одну вспомогательную формулу, позволяющую вычислять общее требуемое количество форсунок (во всех рядах сразу)

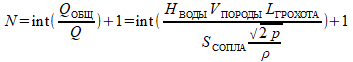
В следующих формулах предполагается «прямоугольное» размещение форсунок, т. е. рядами в количестве N_РЯДОВ по одинаковому количеству форсунок N_{В_РЯД}. Ниже приведена рекомендация по «шахматному» расположению форсунок. Однако общее количество форсунок при таком расположении не изменяется и все полученные ниже формулы применимы и в этом случае с точностью до переноса одной форсунки из ряда в ряд.

Можем получить формулы вычисления недостающих параметров системы орошения для виброгрохота.

Число форсунок в ряду вычисляется по ширине полосы орошения одной форсунки:

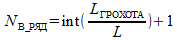
где L вычисляется по формуле (7).

При этом интенсивность орошения, как правило, оказывается недостаточной. Для набора нужной интенсивности устанавливается нужное количество рядов:

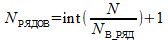
где общее требуемое количество форсунок N вычисляется по формуле (10).

Должно быть задано желаемое количество форсунок в ряд. Тогда высота установки вычисляется через требуемую ширину орошения:

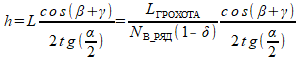
Число требуемых рядов вычисляется по формуле (11) так же, как в предыдущей задаче.

Можно поставить несколько вариантов задач, приводящих к необходимости вычисления требуемого рабочего давления. Здесь рассматривается решение следующей задачи: найти необходимое рабочее давление, зная число необходимых форсунок и величину требуемого увлажнения. В этом случае требуемое давление вычисляется по формуле Бернулли:

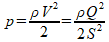
где все величины должны быть взяты в системе Си:

p – давление, результат получается в Па, для перевода в ати нужно разделить на 101300 (Па/ати);

Q – объёмный расход через форсунку, м³/сек. Для использования величины, заданной в л/с, нужно разделить её на 1000 (л/м³);

S – сечение форсунки, м². Для использования величины, заданной в мм², нужно разделить её на 10⁶ (мм²/м²).

Другие возможные задачи на определение давления решаются аналогично.

• Получена формула вычисления расхода воды через форсунку.
• Форсунки рассматриваемой конструкции можно считать распыляющими воду по узкой линии равномерно по отрезку орошения. При известном расходе воды через форсунку задача расчёта увлажнения поверхности становится чисто геометрической.
• Получена формула вычисления увлажнения поверхности в зависимости от геометрических характеристик форсунки, её сечения, высоты установки, давления воды и скорости движения породы.
• Получен алгоритм вычисления требуемого числа форсунок.
• Получен алгоритм вычисления требуемой высоты установки форсунок.
• Получен алгоритм вычисления требуемого давления воды.

• Форсунки желательно устанавливать с минимальным перекрытием полосы орошения.
• Для компенсации возможной неравномерности распределения воды форсункой по ширине полосы орошения возможно устанавливать форсунки в шахматном порядке. Для исключения недостаточного орошения по краям на ширину L/2 необходимо установить через один «чётный» ряд крайние форсунки с линией орошения под углом 60º к перпендикуляру скорости движения породы. Каждая такая форсунка обеспечивает двойное орошение поверхности в своей полосе по сравнению с соседними. Общее количество требуемых форсунок в этом случае не изменяется.
• Угол наклона факела воды к горизонту выбирается произвольно в зависимости от технологических требований.
• Давление должно быть не ниже минимально допустимого для данной форсунки. При необходимости снижения расхода воды на одну форсунку следует применять форсунки меньшего сечения (6 мм.) со средним давлением из рабочего диапазона.